Publications

Competition between Energy and Dynamics in Memory Formation

Phys. Rev. Lett., (2023)

Bistable objects that are pushed between states by an external field are often used as a simple model to study memory formation in disordered materials. Such systems, called hysterons, are typically treated quasistatically. Here, we generalize hysterons to explore the effect of dynamics in a simple spring system with tunable bistability and study how the system chooses a minimum. Changing the timescale of the forcing allows the system to transition between a situation where its fate is determined by following the local energy minimum to one where it is trapped in a shallow well determined by the path taken through configuration space. Oscillatory forcing can lead to transients lasting many cycles, a behavior not possible for a single quasistatic hysteron.

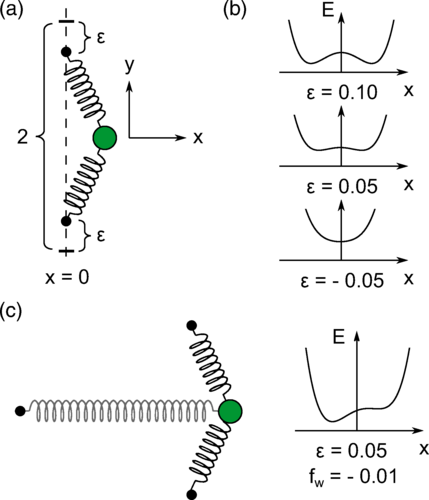
Transient learning degrees of freedom for introducing function in materials

PNAS, (2022)

The introduction of transient degrees of freedom into a system can lead to novel material design and training protocols that guide a system into a desired metastable state. In this approach, some degrees of freedom, which were not initially included in the system dynamics, are first introduced and subsequently removed from the energy minimization process once the desired state is reached. Using this conceptual framework, we create stable jammed packings that exist in exceptionally deep energy minima marked by the absence of low-frequency quasilocalized modes; this added stability persists in the thermodynamic limit.

Deterministic Interrelation Between Elastic Moduli in Critically Elastic Materials

Critically elastic materials - those that are rigid with a single state of self-stress - can be generated from parent systems with two states of self-stress by the removal of one of many constraints. We show that the elastic moduli of the resulting homogeneous and isotropic daughter systems are interrelated by a universal functional form parametrized by properties of the parent. In simulations of both spring networks and packings of soft spheres, judicious choice of parent systems and bond removal allows for the selection of a wide variety of moduli and Poisson's ratios in the critically elastic systems, providing a framework for versatile deterministic selection of mechanical properties.

rigidPy: Rigidity analysis in Python

Computer Physics Communications, (2022)

rigidPy is a Python package that provides a set of tools necessary for studying rigidity and mechanical response in elastic networks. It also includes suitable modules for generating new realizations of networks with applications in glassy systems and protein structures. rigidPy is available freely on GitHub and can be installed using Python Package Index (PyPi). The detailed setup information is provided in this paper, along with an overview of the mathematical framework that has been used in developing the package.

Emergence of zero modes in disordered solids under periodic tiling

Phys. Rev. E, (2022)

In computational models of particle packings with periodic boundary conditions, it is assumed that the packing is attached to exact copies of itself in all possible directions. The periodicity of the boundary then requires that all of the particles' images move together. An infinitely repeated structure, on the other hand, does not necessarily have this constraint. As a consequence, a jammed packing (or a rigid elastic network) under periodic boundary conditions may have a corresponding infinitely repeated lattice representation that is not rigid or indeed may not even be at a local energy minimum. In this manuscript, we prove this claim and discuss ways in which periodic boundary conditions succeed in capturing the physics of repeated structures and where they fall short.

Energetic rigidity I: A unifying theory of mechanical stability

Physical Review E,  (2022)

Rigidity regulates the integrity and function of many physical and biological systems. This is the first of two papers on the origin of rigidity, wherein we propose that “energetic rigidity,” in which all nontrivial deformations raise the energy of a structure, is a more useful notion of rigidity in practice than two more commonly used rigidity tests: Maxwell-Calladine constraint counting (first-order rigidity) and second-order rigidity.  The formalism of energetic rigidity unifies our understanding of mechanical stability and also suggests new avenues for material design.

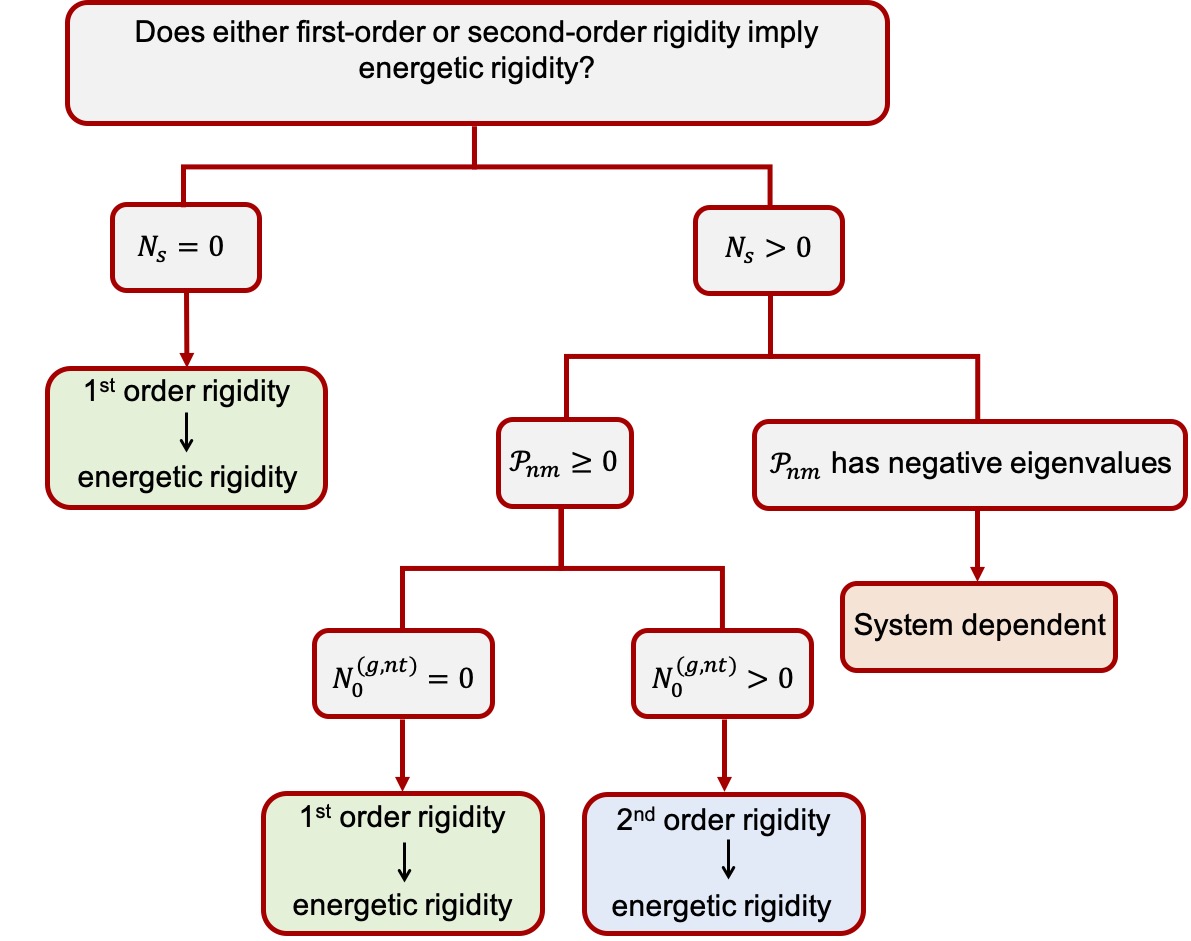
Energetic rigidity II: Applications in examples of biological and underconstrained materials

Physical Review E,  (2022)

This is the second paper devoted to energetic rigidity, in which we apply our formalism to examples in two dimensions: Underconstrained random regular spring networks, vertex models, and jammed packings of soft particles. Spring networks and vertex models are both highly underconstrained, and first-order constraint counting does not predict their rigidity, but second-order rigidity does. In contrast, spherical jammed packings are overconstrained and thus first-order rigid, meaning that constraint counting is equivalent to energetic rigidity as long as prestresses in the system are sufficiently small. 

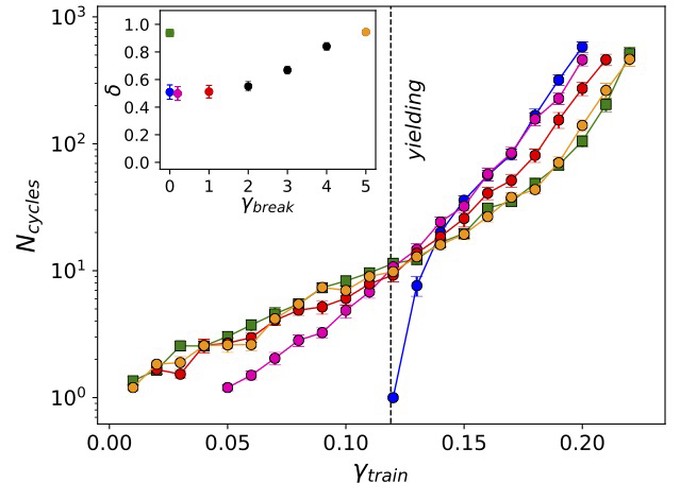
Marginal stability in memory training of jammed solids

Phys. Rev. E,  (2021)

When a jammed sphere packing is repeatedly sheared with cycles of the same strain amplitude, it optimizes its mechanical response to the cyclic driving and stores a memory of it. We study memory by cyclic shear training as a function of the underlying stability of the amorphous structure in marginally stable and highly stable packings, the latter produced by minimizing the potential energy using both positional and radial degrees of freedom. We find that jammed solids need to be marginally stable in order to store a memory by cyclic shear.

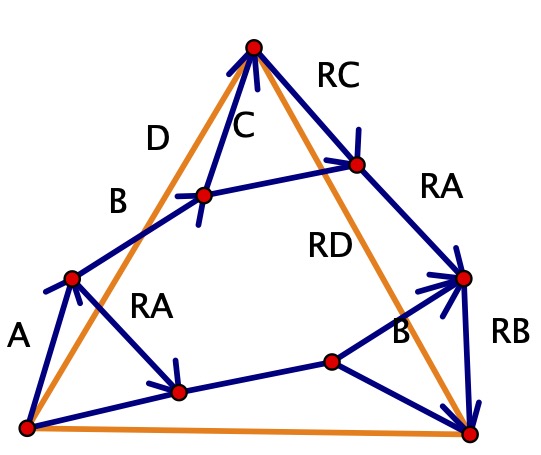
Realizations of Isostatic Material Frameworks

physica status solidi, (2021)

This article studies the set of equivalent realizations of isostatic frameworks and algorithms for finding all such realizations. It is shown that an isostatic framework has an even number of equivalent realizations that preserve edge lengths and connectivity. The complete set of equivalent realizations for a toy framework with pinned boundary in two dimensions is enumerated and the impact of boundary length on the emergence of these realizations is studied. To ameliorate the computational complexity of finding a solution to a large multivariate quadratic system corresponding to the constraints, alternative methods—based on constraint reduction and distance-based covering map or Cayley parameterization of the search space—are presented.

A broader view on jamming: from spring networks to circle packings

Soft Matter, (2019) 

Jamming occurs when objects like grains are packed tightly together (e.g. grain silos). It is highly cooperative and can lead to phenomena like earthquakes, traffic jams, etc. In this paper we point out the paramount importance of the underlying contact network for jammed systems; the network must have one contact in excess of isostaticity and a finite bulk modulus. Isostatic means that the number of degrees of freedom is exactly balanced by the number of constraints. This defines a large class of networks that can be constructed without the necessity of packing particles together compressively (either in the lab or computationally). One such construction, which we explore here, involves setting up the Delaunay triangulation of a Poisson disk sampling and then removing edges to maximize the bulk modulus until the isostatic plus one edge is reached.

Disordered auxetic networks with no reentrant polygons

Phys. Rev. B, (2018)

We reveal significant qualitative differences in the rigidity transition of three types of disordered network materials: randomly diluted spring networks, jammed sphere packings, and stress-relieved networks that are diluted using a protocol that avoids the appearance of floppy regions. The marginal state of jammed and stress-relieved networks are globally isostatic, while marginal randomly diluted networks show both overconstrained and underconstrained regions. When a single bond is added to or removed from these isostatic systems, jammed networks become globally overconstrained or floppy, whereas the effect on stress-relieved networks is more local and limited.

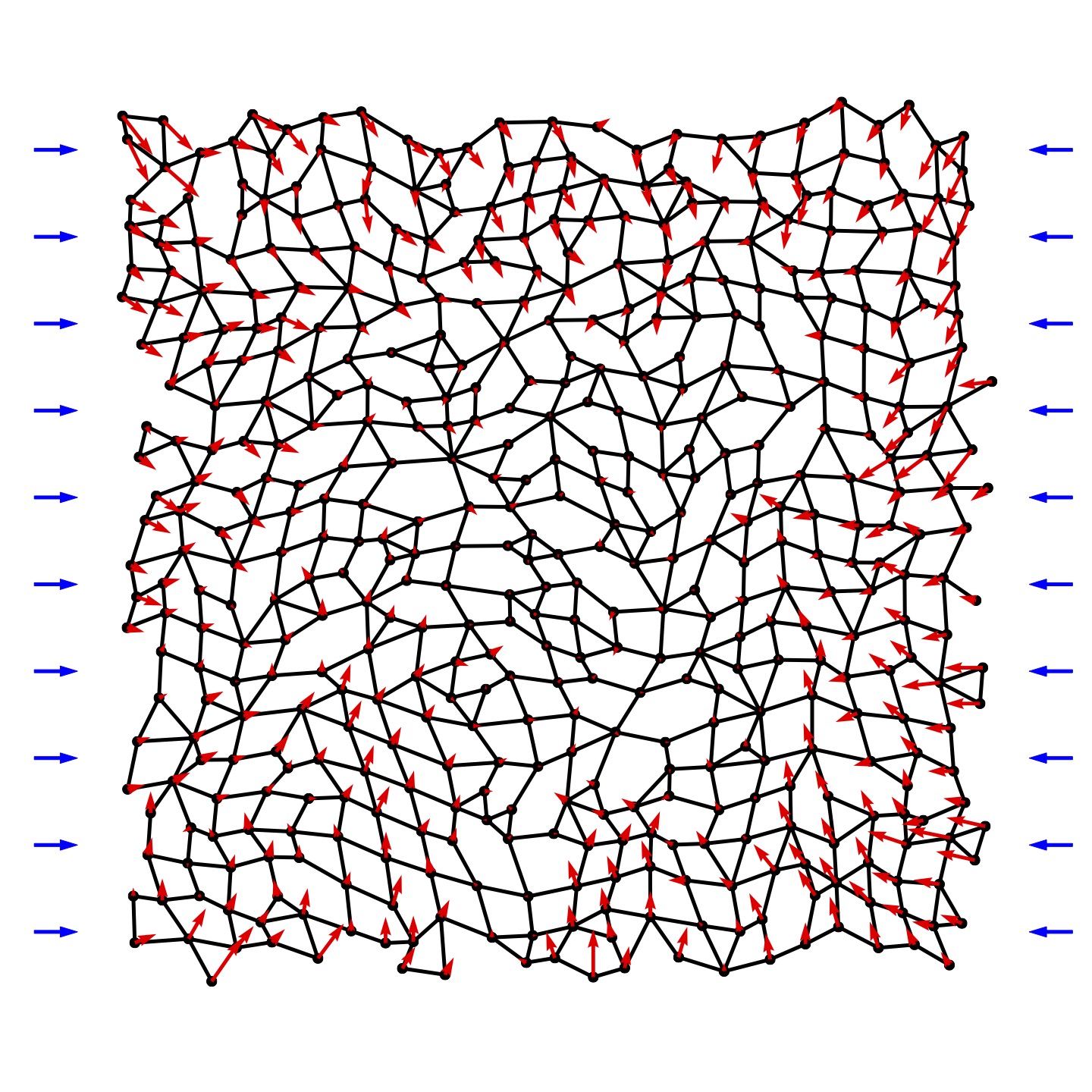
Rigidity Loss in Disordered Systems: Three Scenarios

Phys. Rev. Lett., (2015)

We reveal significant qualitative differences in the rigidity transition of three types of disordered network materials: randomly diluted spring networks, jammed sphere packings, and stress-relieved networks that are diluted using a protocol that avoids the appearance of floppy regions. The marginal state of jammed and stress-relieved networks are globally isostatic, while marginal randomly diluted networks show both overconstrained and underconstrained regions. When a single bond is added to or removed from these isostatic systems, jammed networks become globally overconstrained or floppy, whereas the effect on stress-relieved networks is more local and limited. These differences are also reflected in the linear elastic properties and point to the highly effective and unusual role of global self-organization in jammed sphere packings.